4.4. Оптимизация векторного критерия. Парето-оптимальные решения
4.4. Оптимизация векторного критерия. Парето-оптимальные решения
Рассмотренные выше способы принятия решения предполагают, что в наборе (т.е. векторе) показателей (f1, f2, …,fN) можно тем или иным образом определить показатели более или менее важные (например, за счет весовых коэффициентов). Однако, возможны случаи, когда приоритет показателей установить трудно или невозможно. Тогда среди множества альтернатив X следует искать ту x*, которая лучше всех других альтернатив по всему набору показателей одновременно. Дело осложняется тем, что в подобных случаях часто возникает ситуация, когда, например, x1 лучше x2 по показателю f1, но хуже по показателю f2. Какую альтернативу считать лучшей? Для систематизации рассуждений при выборе альтернатив в подобных условиях, когда нет информации о приоритетах показателей, целесообразно использовать методы принятия решений, основанные на понятиях векторного критерия и Парето-оптимальных решений.
Оптимизация векторного критерия при выборе альтернатив предполагает поиск такой x*, что:
(f1, f2, …,fN) ® max,
где как и раньше мы предполагаем сонаправленность частных показателей и считаем, что вместо max может быть min при соответствующем смысле показателей. Сравни с выбором по всем предыдущим критериям – там везде мы получали какой-то агрегированный показатель F, сформированный из частных f1, f2, …,fN., а потом уже по нему выбирали лучшую альтернативу. Здесь такой F не вводится, т.е. весь набор частных показателей рассматривается как единое целое.
В подобной задаче выделяют два этапа принятия решения: сначала из множества Х отбираются Парето-оптимальные решения ХP, потом уже ЛПР, возможно привлекая дополнительные сведения, с учетом собственных предпочтений выбирает x* из ХP. Как правило множество ХP много меньше, чем Х, поэтому выбирать из него уже значительно проще.
Поясним, что такое Парето-оптимальные решения (еще называют – эффективные решения, недоминируемые решения), проведя аналогию с обычными оптимальными решениями при одном показателе. Пусть имеется только один показатель, по которому сравниваются альтернативы – F. Ясно, что оптимальной по этому показателю будет та альтернатива x*, для которой выполняется условие: F(x*) >= F(x) – оценка альтернативы по показателю лучше (или не хуже), чем оценки F у всех остальных альтернатив. Аналогично и для векторного критерия – альтернатива xp принадлежит множеству Парето-оптимальных, если выполняется условие:
(f1, f2, …,fN) (xp) >= (f1, f2, …,fN) (x),
где x не принадлежит ХP ;
”>=” – означает “больше или равно”.
Эта запись означает, что для всех fi верно fi(xp) >= fi(x) и есть хотя бы один показатель fjтакой, что fj(xp) > fj(x). В этом случае можно говорить, что xp лучше (предпочтительнее), чем x, для чего будем использовать следующую запись: xp } x.
Сами Парето-оптимальные решения являются между собой несравнимыми (по крайней мере по данному набору показателей). Если, например, имеются x1p и x2p, то всегда при fi(x1p) > fi(x2p) имеется и такой показатель, что fj(x1p) < fj(x2p) – т.е. попытка улучшить решение по одному показателю приводит к ухудшению его по другому.
Общий алгоритм поиска Парето-оптимальных решений состоит в последовательном уменьшении исходного множества Х:
1. Выбрать из множества Х первую альтернативу x1 и сформировать множество Х1 из Х. Для этого сравнить x1 со всеми остальными альтернативами. Если есть такое решение x, что x1}x, то x не включаем в Х1 (т.е. оно заведомо не будет Парето-оптимальным).
Если после перебора не нашлось никакого х}x1 , то x1 – включается в ХР. После перебора x1 уже не берется в рассмотрение на следующем шаге и, следовательно, не включается в Х1.
2. Повторяем эти операции, взяв следующую альтернативу - x1 и сформировав на выходе множество Х2 из Х1 и т.д.
Пример. Имеется несколько вариантов проекта станка (см. табл.). Каждый вариант оценивается по балльной шкале одинаковым набором показателей. Приоритет показателей неизвестен. Нужно найти Парето-оптимальные решения.
Таблица
Исходные данные для задачи выбора вариантов проекта станка
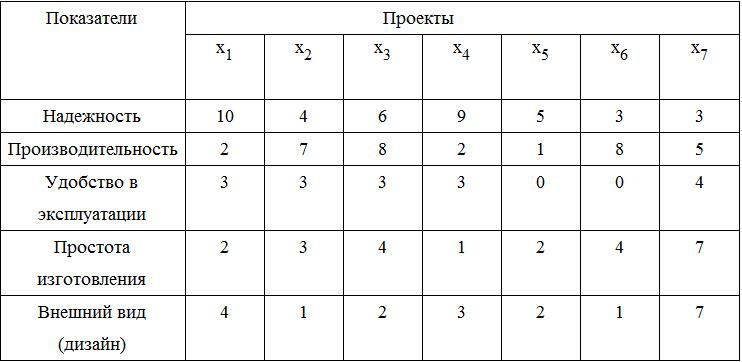
Решение:
1. Возьмем x1. Сравнивая его последовательно с остальными будем выбрасывать те, которые хуже, чем x1. Так, x2, x3 – хуже по Надежности, но лучше по Производительности. Значит, оно уже войдет в Х1. А вот x4 хуже (или равно) по всем показателям, чем x1, значит оно не войдет в Х1. Так же дело обстоит и с x5. В общем на выходе этого шага имеем Х1= { x2, x3, x6, x7} и x1 является Парето-оптимальным, т.к. нет никакого x }x1.
2. Берем из Х1 альтернативу x2. По сравнению с ней x6 , x7 – не хуже, а x3 – даже более предпочтительнее. Значит, x2 – не является Парето-оптимальной, а Х2= { x3, x6, x7}.
3. Берем x3. При этом x6 – хуже ее и, значит x6 не будет включаться в Х3. Альтернатива x7 хуже по первым двум, но лучше по остальным трем показателям, значит она включается в Х3. Так как, нет ни одного x}x3, то x3 также является Парето-оптимальным решенеим.
4. Множество Х3 состоит из всего одной альтернативы x7, которая, очевидно, оказалась не хуже чем остальные уже рассмотренные, т.е. x7 также принадлежит XР.
Таким образом, множество Парето-оптимальных решений в данном примере составляют следующие варианты проектов: XР = { х1, х3, х7 }.
Читать дальше:
#a href="http://www.systematy.ru/articles/45_prinyatie_resheniy_v_usloviyah_riska_i_neopredelennosti"#4.5. Принятие решений в условиях риска и неопределенности#/a#
Похожие статьи:
| 4.3. Критерии и способы принятия решений при оценке полезности альтернатив |
| 28 марта 2012, |
| 4.3. Критерии и способы принятия решений при оценке полезности альтернатив В табл.4.1. для иллюстрации материала приведены численные значения четырех показателей для трех альтернатив X1, ... Читать полностью |
| 4.5. Принятие решений в условиях риска и неопределенности |
| 29 марта 2012, |
| 4.5. Принятие решений в условиях риска и неопределенности Выше мы рассматривали принятие решений с учетом оценки полезности альтернатив. Во многих практических задачах полезность а ... Читать полностью |
| 4.1. Постановка задачи принятия решения |
| 28 марта 2012, |
| 4.1. Постановка задачи принятия решения Роль и место задачи принятия решений (ЗПР) в теории систем и системном анализе показаны в гл. 2. В общем виде постановка задачи принятия решения в ... Читать полностью |
| 3.4.Оптимизационные математические модели |
| 28 марта 2012, |
| 3.4.Оптимизационные математические модели Среди широкого круга задач, решаемых с помощью функциональных математических моделей можно выделить два основных их вида: задачи прямого счета и оптим ... Читать полностью |
| Тема 5. Комплексная автоматизация управления предприятием. Корпоративные ЭИС. Понятие и задачи корпоративной ЭИС. ч.1 |
| 03 июня 2012, |
| Современные достаточно крупные предприятия (организации) характеризуются высокой сложностью процессов управления. Большое количество работников и управленческого персонала, выполняющих существ ... Читать полностью |